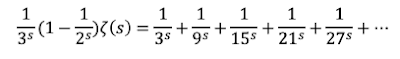La universidad de San Petersburgo, junto a su Academia, era sin duda el principal lugar para la ciencia y el conocimiento en la Rusia zarista. Tras la expulsión de las tropas napoleónicas el país comenzó a notar algunos tímidos cambios sociales, prueba de ello fue la creación de las universidades de Kazán, Kharkov y Moscú. El fruto no se hizo esperar y aparecieron rutilantes figuras en muchos campos de la ciencia. Nosotros fijaremos nuestra atención en la figura de Chebyshev.
Escribo Chebyshev de esa manera, porque es la que parece más aceptada, por lo menos en los buscadores de internet, pero lo he visto escrito: Chebychev, Chebycheff, Tchebycheff, etc... Esto es debido a que se hace una transcripción fonética del cirílico; para que no quede ninguna duda lo dejo escrito tal y como se hace su lengua materna:
PAVNUTY LVOVICH CHEVYSHEV
Пафнуты Львович Чевишев
Puede que sea uno de los matemáticos más importantes de todos los tiempos pues sus contribuciones a diversos campos de la ciencia son fundamentales sobre todo estadística e ingeniería con su famosa desigualdad o sus polinomios para aproximar funciones, pero lo que aquí más nos interesa es su relación con el Teorema de los Números Primos.
Hacia 1849 Chevyshev escribió su primer artículo sobre el tema titulado "A cerca de la función que determina la totalidad de los números primos menores que un límite dado". Lo que hizo fue empezar a manipular el resultado de Euler, que ya hemos visto en entradas anteriores, y que no era más que la consecuencia de aplicar la Criba de Erastóstenes al "Problema de Basilea" de forma genérica.
Donde, como sabemos, el sumatorio recorre todos los "n" (números naturales) y el productorio todos los "p" (números primos), siempre elevados a un mismo número genérico aquí denominado "s". Pues bien, el resultado al que Chevyshev llegó fue sorprendente, porque demostró que la función que Gauss utilizó en el Teorema de los Números Primos, es decir 𝛑(x), estaba acotada por arriba y por abajo:
Posteriormente en 1881 J.J.Silvester refinó el método y obtuvo en una primera aproximación de a=0,95695... y b=1,04425... para valores de x muy altos, por lo que aproximando podríamos decir que 𝛑(x) no difiere más de un ±10% de x/logx.
Si manipulamos la expresión anterior obtenida por Chevishev obtenemos:
obteniendo lo que se llama resultado débil y que nos acota, como hemos mencionado antes, los valores posibles de la función 𝛑(x), pero si esto lo llevamos al límite:
llegamos al denominado resultado fuerte y que no es más que la denominada Ecuación Asintótica de los ℕ (números naturales). ¡Sorprendente!
Estos resultados fueron muy importantes para seguir comprendiendo el Teorema de los Números Primos, y puede que fuera la última vez en la que se utilizaran para ello métodos elementales, como dicen los matemáticos, pues no se usó el poder de las funciones de números complejos.
Estos resultados condujeron a que Chevishev demostrara el famoso postulado de Bertrand el cual dice:
Si n>3 entonces existirá al menos un número primo que cumple la condición n<p<2n.
Dicho de otra manera: "Entre cualquier número y su doble,
siempre hay intercalado, al menos, un número primo".
Posteriormente el genio y joven talento húngaro Paul Erdös, con 18 años de edad logró también demostrarlo de una manera más sencilla y muy ingeniosa pero que se escapa tangencialmente al objetivo de este blog, de todas maneras, puedes encontrar una versión muy sencilla en el siguiente enlace, que es un PDF de la Universidad Nacional Autónoma de México. También logró demostrarlo de otra forma, en este caso recurriendo a las propiedades de la función 𝚪(x) el genial matemático hindú Ramanujan sobre el que se ha realizado una película "El hombre que conocía el infinito" y que recomiendo disfrutar de ella.
También existe una demostración muy asequible a este postulado utilizado el método de inducción, fácilmente entendible y que puede descargarse en: https://arxiv.org/abs/1608.07240
Como podréis comprobar después de tanta demostración ya no debería llamarse postulado...
Paul Erdös
No podemos terminar esta entrada sobre Chevishev sin hablar de la famosa preferencia o sesgo que descubrió en los números primos. El genial matemático ruso hizo lo siguiente:
Dividió los números primos por 4 y fue anotando el resto, tal y como se ve en esta tabla.
En la primera línea aparecen los números primos, en la segunda el resto de dividirlos por 4, como es normal siempre será 1 o 3. En la tercera línea, y esto es de lo que se percató Chevishev, vamos contando las veces que cada uno de los restos aparece. Por ejemplo para el número 29 han aparecido el mismo número de veces el resto 1 y el 3, por lo que ponemos 0, que sería "empate". Para el número 41 ha aparecido más veces el resto 1 que el resto 3 y por eso ponemos 1. Puede comprobarse enseguida que las veces que contamos resto 3 es mucho mayor que las veces que contamos 1. Vemos que a partir del primo 41 los restos 3 cogen la delantera y los 1 no vuelven a aparecer por delante en la cuenta hasta el primo 26.861.
Se ve que los primos tienen querencia o prefieren los restos de división mayores.
Esta prueba también se hizo dividiendo por 3 (restos posibles 2 y 1) obteniendo resultados más abultados, es decir los primos prefieren el resto 2 y este siempre lleva la delantera hasta el 608.981.813.029.
Lo más sorprendente del caso es que esa preferencia por el 3 en vez del 1 no se mantiene, se rompe como, se ha dicho, en el 26.861, pero vuelve a establecerse otra vez para volverse a romper de nuevo y así sucesivamente hasta el infinito. El matemático J. E. Littlewood probó en 1914 que este sesgo es roto continuamente aunque siempre haya un número preferido.
Al tratar con números altos puede ser que sea difícil verlo con claridad pero un par de gráficas nos ayudarán. En esta primero representamos la tabla de arriba, del número 5 al 97, concretamente la cuarta línea de la tabla anterior donde restamos el número de 3's del número de 1's aparecidos hasta el momento.
Conforme aparece más veces el tres, la gráfica se va separando más y más del eje x hacia arriba.
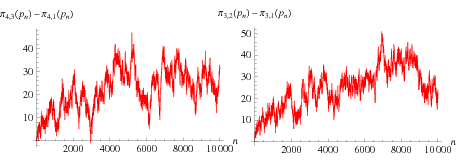
Si en vez de hacer esta gráfica para los números primos menores de 100, como hemos hecho, la hacemos para miles de números primos obtenemos esto:
La de la izquierda es cuando dividimos por 4 y vemos que toca al eje x por el número 26.861 para volverse a mantener siempre por encima, lo que implica que los restos 3 "ganan".
De la misma manera la gráfica de la derecha es para cuando dividimos por tres en este caso los restos 2 se mantienen siempre por encima y no tocarán el eje x hasta el valor 608.981.813.029, como habíamos dicho y que no aparece aquí debido a su enormidad.
De la misma manera la gráfica de la derecha es para cuando dividimos por tres en este caso los restos 2 se mantienen siempre por encima y no tocarán el eje x hasta el valor 608.981.813.029, como habíamos dicho y que no aparece aquí debido a su enormidad.
"El caprichoso comportamiento de los números primos nunca deja de sorprendernos"