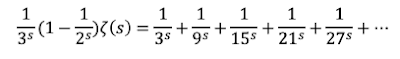La Criba de Eratóstenes

Eratóstenes de Cirene fue un famoso sabio griego nacido en el 276 a.C. y que logró portentosos descubrimientos para aquella época. Entre los más notables:

1. Logró calcular con gran precisión la circunferencia de la Tierra midiendo la sombra que proyectaban dos estacas calcadas en el suelo a medio día en dos ciudades separadas por una gran distancia: Alejadría y Siena (hoy Asuán). Este experimento lo hizo famoso, al menos para nuestra generación, Carl Sagan en su programa Cosmos. Si queréis ver de nuevo este trocito de vídeo aquí tenéis un enlace: Cosmos_Carl_Sagan_Eratóstenes. Este vídeo debería también ser visto por los "terraplanistas".
2. Dedujo la inclinación del eje de la Tierra respecto al Sol (hoy diríamos plano de la ecléctica)
3. Se atrevió a calcular la distancia entre el Sol y la Tierra.
4. Fue la primera persona a la que se le ocurrió intercalar un día adicional cada cuatro años (años bisiestos)
5. Inventó la esfera armilar, fundamental para la navegación y utilizada hasta el siglo XVII.
6. Se dice que levantó mapas con gran precisión y utilizó por primera vez el concepto de cuadrícula cartográfica (algo parecido a meridianos y paralelos).
7. Ideó la denominada Criba de Eratóstenes.

Esfera Armilar

Algunos le denominaron el segundo Platón y puede que sea uno de los sabios más importantes y prolíficos de la época. En su honor se han dado nombres a una montaña submarina, un cráter en la Luna, un asteroide y un periodo geológico lunar denominado Eratosteriano.

Pero lo que nos ha llevado a recordar su figura es la Criba de Eratóstenes que no es más que un sencillo algoritmo para obtener de una manera rápida los números primos menores que un número dado.

Vamos a ver cómo funciona este método con un ejemplo, buscando los primos menores que 100:

• Escribamos los números del 1 al 100 de una manera que nos sea fácil localizarlos, una tabla es una buena opción.
• Tachemos el número 1 porque no es primo. No se considera primo porque no es divisible por dos números como todos los primos. El 1 es sólo divisible por sí mismo. Los primos son divisible por 1 y por sí mismos.
• El siguiente número, el 2, seguro que es primo porque sólo tiene el 1 por debajo. No lo tachamos, pero sí todos sus múltiplos porque no van a ser primos.

• Ahora hagamos lo mismo con el 3, que seguro que también es primo. Luego tachemos sus múltiplos.

• Hagamos lo mismo con el 5.

• Igual con el 7.

• Podemos observar que siempre el primer número que nos vamos encontrando es primo. Ahora hagamos lo mismo con el 11, y vemos que sus múltiplos 22, 33, 44, 55, 66, 77, 88 y 99 ya estaban eliminados.
• Sigamos con el 13 y pasa lo mismo que con el 11 sus múltiplos menores que 100 están ya tachados, eso pasa con el resto.
• Tras la última criba realizada, nos quedan los números: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, que son los primos menores que 100.

Tenemos entonces que los números no tachados son los primos menores que 100. Esto lo hemos hecho de una manera fácil y rápida porque son 100 números, pero se vuelve muy complicado si intentamos hacerlo para 1000 o 10000; ¡no te digo para 10000 o más, un auténtico infierno!

Este método es sencillo para trabajar con cifras bajas.

Pues bien, el genial Euler lo utilizó de una forma original, asombrosa y elegante, propia de un genio como él, con la que posteriormente se llamaría Función Zeta de Riemann y que vimos en la entrada anterior del blog.
Veamos cómo realizó la criba pues es de matemáticas elementales y es muy fácil seguir. Partamos de nuestra ya conocida Función Zeta:

Multipliquemos ambos lados de la igualdad por 1/2ˢ, por lo que:

Ahora restamos la primera expresión de la segunda:

Observándose que la resta ha eliminado todos los denominadores pares de la parte derecha de la igualdad. Siguiendo con la criba procedamos igual con el siguiente término 1/3ˢ, primero multiplicamos por el resultado de la resta anterior:

De nuevo restamos ambas expresiones:

Vemos ahora que los múltiplos de 3 desaparecen tras la resta, como antes había pasado con los múltiplos de 2. Procedamos ahora con los múltiplos de 5, para ello multipliquemos por 1/5ˢ y restemos de nuevo, obteniendo...

La criba ya nos ha quitado lo múltiplos de 2, 3 y 5. Podríamos estar haciendo esto hasta el infinito, por siempre jamás, y entonces obtendríamos:

dónde podemos observar que nos hemos quedado con los primos como denominador en cada paréntesis. El paso genial ahora es que si dividimos a ambos lados de la igualdad por cada uno de los paréntesis nos queda:

El asombroso resultado de Euler puede ser escrito de diversas maneras. Vemos que se relaciona la Función Zeta con el producto infinito de los inversos de unas expresiones que involucran a los números primos.

Escribiéndolo todo de una manera más compacta y recordando que,

Tenemos entonces,

Lo que relaciona una suma infinita (Función Zeta) de "números enteros" con un producto infinito, en este caso de números primos (p significa "número primo").

Esta expresión, denominada Fórmula Producto de Euler, puede también ser utilizada como una demostración alternativa de que el número de primos es infinito, es decir no acaban nunca; si hacemos s=1, como sabemos, la parte izquierda de la igualdad se convierte en la serie armónica y su suma no converge, es infinito. Por lo tanto el otro lado de la igualdad debe ser infinito también. Lo que quiere decir que hay un numero infinito de p (primos).

Función Zeta de Riemann

Comencemos por recordar la anterior entrada "El Problema de Basilea" y que el genial Euler consiguió sorprendentes soluciones, pero sólo para los números pares.

Si hacemos una tabla calculando la suma de bastantes términos obtenemos lo siguiente:

Cuando s toma valor 1 tenemos la serie armónica que sabemos que diverge, es decir que suma infinito. Cuando toma valores pares, tenemos las soluciones que propuso Euler, ¿pero qué ocurre cuando s toma valores impares?

Hasta ahora nadie ha sido capaz de calcular una forma cerrada para esas sumas, aunque se sabe que convergen.

Quizá el único resultado destacable al respecto es la denominada Constante de Apéry, y que no es más que la suma de la serie para s=3, este matemático francés demostró en 1977 que la suma es un número irracional. Sobre esta constante, y como curiosidad matemática podemos decir que su recíproco 1/1,202056903159... corresponde con la probabilidad de que eligiendo tres números enteros al azar, no tengan ningún factor (cuando los descomponemos en factores primos) en común. Esta probabilidad es aproximadamente del 83% es decir: 1/1,202056903159..=0,831907372580...

Volviendo a al título de esta entrada, la Función Zeta de Riemann tiene una forma que ya dominamos y que no es más que el caso general de la serie originaria del Problema de Basilea:

Como a los matemáticos les gusta ahorrar escritura en el sumatorio ponen sólo n en la parte inferior pero es exactamente lo mismo que hemos visto antes: suma infinita para todos los números naturales, 1, 2, 3, ... También es muy común encontrarse la serie escrita de la manera alternativa:

La serie converge para cualquier número entero mayor que 1. Pero ¿qué ocurre si hacemos que s no sea un número entero? Si nos vamos acercando cada vez más a 1 dónde sabemos que la serie diverge, el resultado de la suma es cada vez mayor:

Conforme nos acercamos a s=1 el resultado de la suma se dispara a valores enormemente altos, lo que indica que la serie no tiende a ningún valor, sencillamente cada vez el resultado de la suma es más disparatadamente grande, tendiendo infinito. Puede que una gráfica de la función nos ayude a verlo todo con mejor en perspectiva.

Para cualquier valor s>1 la serie tiene suma concreta, tendiendo sumar 1 cuando s→∞.

Conforme s→1, las serie tiende a sumar ∞.

Ya tenemos claro cómo funciona la Función Zeta para valores s>1. ¿Pero qué ocurre para valores s<1?

En el caso de que s=0, la serie se nos transforma en:

Y vemos que la suma diverge totalmente, es infinito. Para números negativos, s<0, la cosa es incluso peor.

Comprobamos que para s=-1 y de la misma manera para todos los negativos la suma también diverge. Por lo tanto podemos deducir que la gráfica anterior muestra lo fundamental de la Función Zeta y que no hay nada más, la función solo tiene valores finitos para s>1, dicho de otra manera, el dominio de la función es para todos los valores superiores a 1. ¡Y se acabó!

¿Pero estamos en lo cierto?

Evidentemente no, Riemann tuvo una genial idea de extender la función a otro tipo de números y no quedándose sólo en los Reales.

Esto ya lo veremos en otra entrada, pero os dejo una imagen con una pista sobre la idea de Riemann.